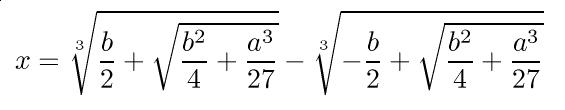Másodfokú Egyenlet Megoldóképlete Bizonyítás

Másodfokú egyenlet megoldóképlete diszkrimináns viéte formulák 4 perc olvasás állítás.

Másodfokú egyenlet megoldóképlete bizonyítás. Azért hogy ne kelljen a szorzattá alakítással minden másodfokú egyenletnél hosszadalmasan dolgoznunk felírjuk a másodfokú egyenletek 0 ra redukált rendezett általános alakját és azzal végezzük el a szorzattá alakítást majd az így kapott eredményt receptszerűen használjuk. Ezek alapján a b x együtthatója a c pedig konstans állandó vagyis rögzített szám értéke nem változik. A középkorból elsősorban a francia viete nevét említhetjük aki már szimbólumok segítségével igyekezett. Amennyiben az egyenletben mínusz jel található akkor ezen változót mint negativ számot írja be.

Ax 2 bx c 0 ahol a 0. Az alakú másodfokú egyenlet megoldóképlete. Nagyon figyelj arra hogy az egyenlet mindig nullára legyen rendezve. X 1 0 azaz x 1 1.

Legyen adott egy alakú másodfokú egyenlet ahol az együtthatók valós számok továbbá ekkor az egyenlet gyökei ha értelmezve vannak. Egyenlet másik gyöke pedig x 3 2 0 azaz x 2 1 5 ez jó megoldás. Ezután az együtthatók sorrendjére figyelj. Az a a b és a c pedig az általános alakban lévő számok.

A másodfokú egyenlet általános kanonikus alakja tehát. Mind az 1300 db ingyenes és reklámmentes videó megtalálható itt. A másodfokú egyenlet megoldóképletét először a mai alakhoz hasonló egységes formában a felesleges együtthatókkal kapcsolatos esetszétválasztások nélkül michael stifel 1487 1567 írta fel bár a mainál sokkal esetlenebb jelölésekkel. Az a b c betűket együtthatóknak nevezzük.

Azt már megállapítottuk hogy. Egyenlet egyik gyöke tehát. Mindig álljon elöl az x négyzetes tag aztán az x es tag majd a konstans vagyis a c értéke. A kalkulátorok kvadratikus egyenleteket old meg.

De ez nem pozitív szám. A másodfokú egyenlet megoldóképlete így néz ki. A másodfokú egyenletnek létezik egy úgynevezett megoldóképlete. Az a x 2 együtthatója.

Ezeket a számokat helyettesítjük be a megoldóképletbe. Nézzük meg hogyan kell alkalmazni a képletet másodfokú egyenletekre. 2000 ből való mezopotámiában talált leletek igazolják hogy már ekkor is meg tudtak oldani másodfokú egyenletet is. Irja be a megadott alak szerint a formába.

A másodfokú egyenlet diszkriminánsa. A másodfokú függvény általános képlete. A matematikában a másodfokú egyenlet egy olyan egyenlet amely ekvivalens algebrai átalakításokkal olyan egyenlet alakjára hozható melynek egyik oldalán másodfokú polinom szerepel tehát az ismeretlen x legmagasabb hatványa a négyzet a másik oldalán nulla redukált alak. A gyöktényezős alak és a megoldóképlet.

Ez a másodfokú egyenlet megoldóképlete.